1.Giriş

Matematiği empirik bilimlerden ayıran,ona bilimlerin kraliçesi diye ün kazandıran en belirgin özellik hiç kuşkusuz matematiğin kesinliği ve eriştiği sonuçların zorunluluğudur.Empirik bilimlerin en gelişmiş olanında bile bu kesinlik  ve zorunluk yoktur.Empirik olgulara ilişkin bir hipotezin doğruluğu,dayandığı kanıtlara göre en çok yüksek bir olasılıktır,yoksa bir kesinlik olamaz. Başka bir değişle, bilimde bir hipotez ne denli kanıtlanmış olursa olsun, bir gün yeni gözlemler karşısında yanlışlanma olasılığından kurtulamaz.Böylece, tüm bilimsel hipotez ve teoriler,geçici nitelikte olup,olgulara ters düşmedikleri sürece doğru sayılırlar.Oysa matematikte bir teorem bir kez ispatlanınca kesinlik kazanır;ne denli ters düşerse düşsün hiçbir gözlem karşısında asla sarsılmaz. Bu yazının amacı “matematiksel kesinlik” diye bilinen bu özelliği,geometriyi örnek alarak tanıtlamak,geometrik teorilerin geçerliğisorununu aydınlatmaya çalışmak ve fiziksel uzayın  yapısına ilişkin bilgilerimiz yönünden bu teorilerin önemini belirtmektir.

Matematiksel doğruluğun niteliğini, onu sağlayan yöntemi inceleyerekanlayabiliriz.Bu konuda sözü uzatmayacağım: Bu yöntem bir önermenin başka bir önerme ya da önermelere başvurularak mantıksal çıkarımla ispatlanmasını içerir.Açıktır ki, ispatta,bazı önermeleri ispatlamaksızın doğru saymak gereği vardır;yoksa sonu gelmeyen bir geriye gidişten kurtulunamaz. Tüm matematiksel teorilerde temel varsayımları oluşturan bu tür önermelere  ilişkin oldukları teorinin aksiyom veya postulat’ları (bu iki terimi eş anlamda kullanacağız) denir. Matematikte aksiyomatik bir sistemin tarihsel ilk örneğini geometri vermiştir. Nevarki, Euclid’in kurduğu sistemde teoremlerini ispatlamada dayandığı postulatlar,geometrisinin tüm önermelerini ispatlamaya yeterli değildir.Bu nedenle Euclid sistemi çağımzda bir çok kez ele alınarak gözden geçirilmiş,daha tam ve yeterli postulatlar konmuştur.Bunlar arasında Euclid sistemini en yakından izleyeni belki de Hilbert’in oluşturduğu sistemdir.

 2.Euclid Postulatlarının Yetersizliği

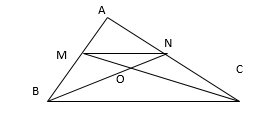
Euclid postulatlarının yetersizliği modern matematikte aksiyomatik metod yönünden can alıcı bir noktayı su üstüne çıkarmaktadır.Bir teorinin postulatları bir kez konduktan sonra,onların çerçevesi dışına çıkamaz;teorinin tüm diğer önermelerinin mantıksal çıkarımı ancak bu postulatlara dayanılarak yapılar;fiziksel uzayda katı cisimlerin davranışlarına ilişkin herhangi bir apaçıklık duygusuna,ya da geometrik şekillerin özelliklerine başvurulamaz, yaşantı ve deneylerimize yer verilemez. Gerçi bu tür şeyler,bir teoremin ispatını bulmada bize yardımcı olabilir,fakat ispatın dayanakları olarak ileri sürülemez. Bu nokta özllikle geometride önemlidir;çünkü,geometrik şekiller ve ilişkiler üzerindeki sezgi ve yaşantımız,ne postulatlar arasında yer alan ne de onlara dayanılarak ispatlanabilen birtakım üstü örtük varsayımlar kullanmaya bizi itebilir.Şu örneği alalım:Bir üçgende kenarları iki eşit parçaya ayıran üç kenar ortay,her birini 1:2 oranında bölen bir noktada kesişirler. Bu teoremi ispatlamak için,ilkin ABC diye aldığımız herhangi bir üçgende (şekile bakınız),AB ve AC’nin ortalarını birleştiren MN  doğru parçasının, BC’ye paralel olduğunu,bu nedenle onun yarısı kadar uzunlukta olduğunu gösteririz.Sonra BN ve CM doğruları çizilir;MON ve  BOC üçgenlerinin incelenmesi bizi teoremin ispatına götürür.Bu işlemde genellikle  BN ve CM doğrularının B ve N ile C ve M arasında yer alan O noktasında kesiştiği kabul edilir.Bu varsayım geometrik sezgiye dayanır. Euclid’in postulatlarından çıkarsanamaz. Sezgiden bağımsız,ispatlanabilir bir önerme niteliği alabilmesi için Euclid’in postulatlarına özel bazı postulatların eklenmesi gerekmiştir. Örneğin bunlardan biri, “A,B,C bir doğru üzerinde noktalar ise ve B noktası A ile C arasında ise,B noktası aynı zamanda C ile A arasındadır” iddiasını dile getirmektedir.İspatta, bu denli önemsiz bir varsayıma bile göz yumulamaz; başta konan postulatlar,tüm önermelerin mantıksal çıkarsamasına elverecek şekilde tam olmalıdır.

Başka bir örneği de şu önermede bulmaktayız: iki kenar ve bunların oluşturduğu iç açıda eş olan üçgenler birbirleriyle çakışır.Euclid geometrisinde bu önerme bir teorem olarak ortaya konmuştur.Ne var ki, verilen ispat şekilleri hareket ve birbirinin üstüne konması düşüncelerinden yararlanmakta, böylece de katı cisimlere ilişkin deneylerimize ve geometrik sezgimize dayanan üstü örtük varsayımları içermektedir.Oysa bu varsayımları Euclid Postulatlarından çıkarsamaya olanak yoktur.Bu nedenledir ki, Hilbert sisteminde bu önerme (daha doğrusu önermenin bir bölümü) belirtik olarak postulatlar arasında yer almıştır.

3.Matematiksel Kesinlik

Matematiksel kesinliği sağlayan şey işte matematik ispatın bu salt dedüktif niteliğidir. Bir teoremin ispatı (örneğin,üçgenin iç açılarının toplamı ile ilgili Önermenin ispatı)o teoremin bir önerme olarak doğruluğunu değil,birtakım  postulatlardan çıkarılabilir olduğunu gösterir; postulatlar doğru ise teoremin doğruluğu kesinlik kazanır.Bu nedenle,matematikte her teoremi şu biçimde yazabiliriz.(Formülde P’ler postulatları,T postulatların içerdiği teoremi,
\( \to \) ise koşulsal ilişkiyi simgelemektedir.):
$$\left( {{P_1},{P_2},{P_3}, \cdots ,{P_N}} \right) \to T$$
Şimdi matematiksel ispatın bu kesin ve zorunlu karakterini biraz daha açıklayalım.

Mantıksal çıkarımların belirgin niteliği şudur:Ulaşılan sonuç hareket noktası postulatların içeriğini ya tümüyle ya da bir bölümü ile dile getirmekten öteye geçemez.Basit bir örnekle bunu şöyle gösterebiliriz: “Bu şekil dik açılı bir üçgendir,” öncülünden “Bu şekil bir üçgendir.” sonucu mantıksal olarak çıkar.Öncül doğru ise,sonuç zorunlu olarak doğrudur.Ancak görüldüğü gibi sonuç öncülü hiç değilse bir bölümü ile yinelemekten öteye geçmemektedir. Gene, “2 dışındaki tüm asal sayılar tek sayılardır.” ve “n, 2’den farklı bir asal sayıdır.” öncüllerinden “n bir tek sayıdır” sonucu mantıksal olarak çıkar.Ne var ki,zorunlu olan bu sonuç da öncüllerin bir parçasını dile getirmekle kalmaktadır.Bu tüm mantıksal çıkarımların değişmez özelliğidir.Buna bakarak,matematiksel ispatın biricik yöntemi olan dedüktif çıkarımı bir kavramsal çözümleme tekniği diye niteleyebiliriz:Öncüllerde saklı olan savları açığa çıkaran,üstü örtük olanı belirtik yapan bir teknik.Öyle bir teknik ki,bir  çıkarımda öncülleri kabul etmekle,daha neyi ya da neleri kabul ettiğimizi bize göstermektedir.Ancak unutmayalım ki,bir teorem(ispatlanan önerme) içerik yönünden postulatlara yeni bir şey eklemek şöyle dursun,çoğu kez onları eksik bir yenilemeden öteye geçmez.

Tüm matematikselispatlar birtakım postulatlardan mantıksal çıkarımlara dayandığından,geometrideki Pythagoras teoremi gibi bir teoremin,dayandığı postulatlar bakımından nesnel ya da kuramsal yeni hiçbir şey ileri sürmediği açıktır. Çıkarımın,postularda farkına varmadığımız bir ilişkiyi ortaya çıkarması bize yeni bir şeye ulaştığımız duygusunu verebilir,ancak bu mantıksal değil,salt psikolojik bir yeniliktir.

Matematiğe özgü kesinliğin niteliği şimdi açıktır: Bir teoremin kesinliği çıkarılmış olduğu postulatlara bağıldır; postulatlar doğru ise teoremin doğruluğu zorunludur.Çünkü teorem,yukarıda belirttiğimiz üzere,postulatlarda ileri sürüleni tam olmasa da yinelemekten ileri geçmez.Böyle koşullu türden bir doğruluğun ise olgulara ilişkin bir içeriği olmadığı,bu nedenle de empirik hiçbir bulgu ile ters düşmeyeceği açıktır.Oysa empirik bilimlerde hipotez ya da teoriler ne denli kanıtlanmış olursa alsunlar,yeni bazı olgulara ters düşüp yalnışlanma olasılığından kurtulamazlar.Matematiksel doğruluk,salt olgusal ya da empirik içerikten yoksun olduğu için kaçınılmaz ve kesindir.Koşullu biçimde oluşturulan herhangi geometrik bir teorem,mantık deyimiyle analitik niteliklidir;doğruluğu a priori’dir.Başka bir deyişle bu teoremin doğruluğunu,empirik verilere başvurmaksızın salt mantık kuralları aracılığı ile kanıtlayabiliriz.

4. Postulatlar ve Doğrular

Denebilir ki,geometrik doğruluk üzerindeki bu düşüncelerimiz konunun sadece yarısını yansıtmaktadır. Gerçekten de geometrik ispat bir önermeyi koşullu olarak (yani postulatları doğru sayma koşullarıyla) ileri sürmemizi sağlıyor ama postulatları kendi başlarına doğru sayarsak,onların mantıksal sonuçları olan teoremleri de koşulsuz olarak doğru saymamız doğru olmaz mı? Örneğin,iki noktanın onları birleştiren bir ve yalnız bir doğruyu belirlediği önermesi,ya da,herhangi bir üçgende iç açıların toplamı iki dik açının toplamına eşittir,önermesi koşulsuz birer savı dile getirmiyorlar mı?İlk bakışta öyle görünseler de aslında öyle olmadıklarını,geometrinin aksiyomatik kuruluşuna ilişkin iki önemli noktayı gözden geçirdiğimizde,anlayacağız.

İlk nokta,Euclid geometrisiyle bağdaşmayan birtakım başka geometrilerin ortaya çıkmış olmasına ilişkindir.Euclid geometrisinde doğru olan örneğin biraz önce sözünü ettiğimiz iki önerme,bu yeni sistemlerde yalnıştır.Euclid’ci olmayan bu sistemlerin bazı temel özelliklerini kısaca belirtmekte yarar vardır. Euclid geometrisinin dayandığı postulatlar arasında ünlü paralel postulatı(herhangi bir doğru dışındaki bir noktadan o doğruya bir ve yalnız bir paralel doğru geçer) da vardır.Bu postulat,ötekilerden çok daha az basit ve sezgisel olarak daha az akla yakın olduğundan,onun bir aksıyom olarak kabul edilmesinin gerekli olmadığını göstermek için tarih boyunca pek çok girişimler yapılmıştır.Ne var ki,paralel postulatı bir teorem olarak ispat yolundaki tüm çabalar boşa çıkmış,sonunda onu Euclid’in diğer postulatlarından (hatta bunların daha tam olan formülasyonlarından)çıkarsamaya olanak olmadığı kesinlikle kanıtlanmıştır.Öyle ki paralel postulatı yerine onunla çelişen başka bir postulatı,(örneğin,”herhangi bir doğru dışındaki bir noktadan o doğruya hiç değilse iki doğru paralel geçer,”önermesini)koyduğumuzda  mantıksal tutarlığı tam yeni bir geometrik teori elde edebilmekteyiz.”Hiperbolik Geometri”denen bu ilk Euclid’ci olmayan geometriyi geçen yüzyılın ilk 20 yılında bir Rus olan N.I.Lobaçhevsky ile bir Macar olan J.Bolyai  kurmuştur.Daha sonra “eliptik” denen bir başka geometrinin ortaya çıktığını görüyoruz. Bir Alman olan Riemann kurduğu bu sistemde paralel postulatının yerini, hiçbir doğrunun paraleli yoktur,önermesi alır. (Ancak,Riemann sisteminin tutarlılığını sağlamak için bu önermenin benimsenmesiyle birlikte diğer Euclid postulatlarında da bazı değişikliklere ihtiyaç duyulmuştur)Kuşkusuz bu yeni geometrilerin pek çok teoremleri Euclid teoremlerinden farklı olacaktır.Örneğin,iki boyutlu hiperbolik geometride “herhangi bir doğruya dışındaki bir noktadan sonsuz sayıda paralel doğru geçer”,önermesi bir teoremdir. Bunun gibi, “herhangi bir üçgenin iç açılarının toplamıiki dik açının toplamından azdır” önermesi de bir teoremdir. Eliptik geometride ise,tam tersine,üçgenin iç açıları toplamı daima iki açıdan büyüktür; birbirine paralel iki doğru yoktur.Ayrıca yeni geometrilerde (Euclid geometrisinde daima olduğu gibi) iki farklı nokta onları bağlayan bir doğruyu belirlerse de belli bazı nokta çiftleri var ki,bunları sonsuz sayıda değişik doğrular birbirine bağlar.Bunun bir örneğini,doğru çizgi kavramını  büyük çember olarak yorumladığımızda küre yüzünün temsil ettiği iki boyutlu eğik uzayın yapısında bulmaktayız.Böyle bir uzayda, verilen herhangi iki büyük çemberkesiştiğinden, paralel doğrular yoktur;küre çapının uç noktalarının, sonsuz sayıda değişik “doğrular” birbirine bağlar:bir üçgenin iç açılarının toplamı da daima iki dik açıdan fazladır.Gene,böyle bir uzayda,bir çemberin uzunluğu ile çapının bölümü daima 2 pi’den azdır.

Euclid’ci olmayan geometriler sadece eliptik ve hiperbolik geometriler değildir;daha başka çeşitleri de oluşturulmuştur.İlerde,gene Riemann’ın kurduğu Euclid’ci olmayan çok daha genel bir sisteme değineceğiz.

Modern matematikte farklı geometrilerin ortaya çıkmış olması, matematikte postulatların doğruluğu ileri sürülerek işe başlanmadığını gösterir.Matematiği ilgilendiren şey sadece şudur:Verilen postulatların mantıksal(dedüktif) sonuçlarını çıkarmak.Teoremlerin zorunlu görünen doğrulukları  postulatların doğruluğuna bağlı kalmaktadır.

Matematiğin, dayandığı postulatların doğru olduğunu ileri sürmediğini gösteren ikinci bir gözlem de geometri kavramlarının statüsüyle ilgilidir. Aksiyomatik her sistemde, önermeler üzerinde yürütülen, kavramlar üzerinde yürütülen işlem arasında yakın bir koşutluk vardır.Daha önce de belirttiğimiz gibi önermeler iki gruba ayrılır: İspatlanmaksızın alınan postulatlat,portulatlara dayanarak ispatlanan teoremler. Aynı şekilde kavramlar da iki gruba ayrılır: Tanımlanmaksızın alınan ilkel ya da temel kavramlar, ilkel terimlere dayanılarak tanımlanan kavramlar. (Bir takım kavramların tanımlanmaksızın sisteme alınması, sonsuz-geri gidişe düşmemek için gereklidir.) Benzerlik bu kadarlada kalmamaktadır: Nasıl ki bir tek teori (Örneğin Euclid geometrisi) için kurumsal olarak sonsuz çoklukta değişik postulat sistemi seçmeye olanak varsa, bunun gibi, sonsuz çoklukta değişik ilkel terimlerden seçme olanağı da vardır. Her zaman değil ama çok kez, bir teorinin değişik aksiyomatikleştirilmesi değişik postulatları gerektirdiği gibi değişik ilkel terimler de gerektirir. Hilbert’in düzlem geometriyi oksiyomatikleştirmesi altı ilkel terim içermiştir: nokta, virgül, doğru(bir noktanın bir doğru üzerine)düşmesi,(bir doğru üzerindeki üç noktanın ilişkisi olarak)arasında olma,doğru parçalarının çakışırlığı,ve açıların çakışırlığı(Hilbert sisteminde üç boyutlu geometri için iki ilkel terime daha ihtiyaç vardır: Düzlem,bir noktanın bir düzleme düşmesi).Geometrinin açı,üçgen,çember,vb. gibi tüm diğer terimleri ilkel terimlere dayanılarak tanımlanan terimlerdir. Ancak,ilkel terimler tanımlanmadığına göre onlara nasıl bir anlam verebiliriz,diye sorulabilir.Bunun yanıtı,onlara belli herhangi bir anlam vermenin gereksiz olduğudur. Gerçi, “nokta”, “doğru”,vb. terimler bildiğimiz bir takım anlamlar taşırlar; ne var ki, bu terimlerin yer aldığı önermelerin geçerliği bu anlamlardan tümüyle bağımsızdır. Gerçekten de Euclid geometrisinde “nokta”, “doğru”, “üzerine düşme”, “arasında olma”,vb.terimler yerine”1.tür nesne”, “2.tür nesne”,”1 no lu ilşki”,”2 no lu ilişki” vb. gibi nötr terimler koyduğumuzu düşünelim.Şimdi ilkel terimlerini değiştirdiğimiz bu geometriyi alışık olduğumuz anlamlarını bilmeyen uzman bir mantıkçı ya da matematikçiye sunarsak ne olur?Bu uzman kişi için tüm ispatlar geçerliğini korur.Nedenini daha önce de açıklamıştık:En sıkı biçimiyle bir ispat terimlerin bilinen anlamlarına asla başvurmaksızın aksiyomlardan dedüktif bir çıkarım yapmaktır.Görülüyor ki aksiyomastik bir teorinin ilkel terimlerine belirli anlam verme gereği yoktur:bu nedenle, mantıksal olarak kurulan geometrik bir sistemin ilkel terimlerine mantıksal değişgen gözüyle bakılabilir.

Demek oluyor ki,geometride postulatların doğruluğunun ileri sürüldüğü söylenemez; çünkü postulatlar belirli hiçbir anlamı olmayan kavramlarla oluşturulmuştur. Bir takım değişkenleri içeren postulatlar ise ne doğru ne de yanlıştır! Modern mantığa uygun deyişle, postulatlar önerme değil, ancak değişken terimlerden oluşturulan önerme kalıpları(ya da önerme fonksiyonları)dır. Bu şunuda göstermektedir ki, geometrinin postulatlarını ”apaçık doğrular” saymak da yalnıştır. Çünkü bir savın olmadığı yerde apaçık doğruluktan da söz edilemez.

5.Saf ve Fiziksel Geometri

Geometri bu anlayış içinde salt formel bir disiplindir:buna saf geometride diyeceğiz. O halde, saf geometri(ister Euclid’ci isterse Euclid’ci olmayan türden olsun)’nin belirli bir konusu yoktur; özellikle fiziksel uzaya ilişkin bir sav içermemektedir. Tüm teoremleri analitiktir; olgusal içerikten yoksun olmaları nedeniyle kesinlikle doğrudurlar.Saf geometrinin anlamını daha iyi belirlemek için film yapımcılarının baş vurdukları bir söz biçimini kullanabiliriz:İlkel kavramlarla onların geometrik şekillere ilişkin alıştığımız anlamları arasında herhangi bir benzerlik sadece rastlantıdır; postulatlarımız ne geometrik şekilleri, ne fiziksel uzayın özelliklerini, ne de cisimlerin ilişkilerini dile getirmektedir.

Ne var ki, film yapımcılarının inkarı gibi hiç değilse Euclid  geometrisi için ileri sürülen bu saflık savı da pek inandırıcı görülmüyor:en azından tarihsel olarak geçerli değildir.Kökeninde bu geometri alan ölçmeye ilişkin ve astronominin gelişmesiyle ortaya çıkan bir takım empirik buluşların genellemelerine dayanır. Bu açıdan bakılınca, geometri olgusal içeriklidir. Fiziksel uzayın yapı teorisi, ya da  kısaca fiziksel geometri adını verebileceğimiz empirik bir bilimdir. Öyle ise saf geometri ile fiziksel geometri arasındaki ilişki nedir?

Fizikçi,fiziksel cisimlere ilişkin önermelerinde nokta, doğru gibi kavramları kullandığında, bu terimlere aşağı yukarı belirli somut anlamlar verir. Onun kullanımında”nokta” iğne uçları,kesişen saçlar gibi nesnelerin örneklediği noktaları adlandırır. Aynı şekilde ”doğru” terimi gergin ipliklerin ya da türdeş bir ortamda güneş ışınlarının örneklediği nesnelerin adıdır. Fiziksel geometeride tüm diğer terimlerin de böyle somut fiziksel anlamları vardır. Şimdi,buna bakarak, fiziksel geometriyi, saf geometrinin(modern mantığındilini kullanarak) semantik bir yorumu sayabiliriz. Daha genel bir değişle diyebiliriz ki saf matematiksel bir teorinin semantik bir yorumu, teorideki her ilkel terime (dolayısıyla her tanımlanmış terime) belirli bir anlam vermek demektir. Fiziksel geometri söz konusu olduğunda verilen anlam biraz önce de belirttiğimiz gibi fiziksel niteliktedir.İstersek geometriye aritmetik bir yorum da verebiliriz; bunun için ilkel terimlere aritmetik anlam vermek yeter. Geometrinin aritmetik yorumu, sistemin tutarlılık ve diğer mantıksal özelliklerini incelemek yönünden son derece önemlidir. Ancak bu konuyu burada ele almayacağız.

Geometrik teorinin başlangıçta yorumlanmamış (değişken) ilkel terimlerine daha sonra verilen fiziksel anlamlar, dolaylı yoldan, teorinin tüm diğer tanımlanmış terimlerine geçer; böylece bu terimlerle formüle edilmiş postulatlarla teoremlerde birer önerme kalıbı değil, fiziksel anlamları belli, yanlış ya da doğru oldukları anlamlı olarak sorulabilen birer önermedir. Örneğin, Euclid  Geometrisinde yorumlanmamış şu postulatı ele alalım:x,y gibi  1’inci türden her iki nesneye karşılık 2’nci türden 1 gibi nesne vardır, öyle ki hem 0  hem y,  1 ile bir no’lu ilişki içindedir.Bu postulat da geçen üç değişgen terim yorumlanmadıkça postulatın doğru olup olmadığını sormanın anlamı yoktur.Ama fiziksel bir yorumla postulat şöyle bir önermeye dönüşür:x:y gibi herhangi bir fiziksel nokta için bir harfle 1 gibi fiziksel bir doğru vardır,öyle ki hem x, hem y 1 üzerinde bulunur. Bir fiziksel hipotez niteliğinde olan  bu önermenin doğru olup olmadığı anlamlı olarak sorulabilir. Aynı şekilde üçgenin iç açılarının toplamına ilişkin teorem,üç ışık ışını ile çevrili kapalı bir şekli (fiziksel anlamda) iç açılarının toplamı iki dik açıya eşittir savına dönüştürülebilir.

Böylece,herhangi saf geometrik bir teoriyi (Euclid’ci olsun veya olmasın) fiziksel yorumlamayla bir fizik hipotezleri sistemine dönüştürebiliriz.Sistemi oluşturan hipotezlerin doğru olması halinde fiziksel uzayın yapısına ilişkin bir teori ortaya çıkmış olur.Fakat fiziksel olarak yorumlanmış bir geometrik teorinin olgusal doğruluk sorunu,salt matematiğin değil empirik bilimin de sorunudur; sistematik gözlem ya da deneye başvurularak çözümlenebilir ancak. Bu konuda matematikçinin ileri sürebileceği tek sav şu olabilir:Teorinin fiziksel olarak yorumlanmış tüm postulatları doğru ise teoremleri de zorunlu olarak doğrudur, çünkü teoremler onların mantıksal sonuçlarıdır. Buna bakarak denebilir ki fiziksel uzayın yapısı yönünden Euclid’ci veya Euclid’ci olmadığını saptamak için, yapmamız gereken tek şey fiziksel yorumlanmış postulatları test etmektir. Ne var ki, bunu doğrudan yapmaya pek olanak yoktur; fizik teorilerinin pek çoğunda olduğu gibi geometride de bu temel hipotezler deneysel yoldan yoklanmaya elverişli değildir. Özellikle, Hilbert’in  Euclid geometrisi sisteminde bir doğru üzerinde bazı sonsuz nokta kümelerine ilişkin Cantor‘un süreklilik aksiyomu ile paralel aksiyom bu türden hipotezlerdir.Bu nedenle, bilimsel teoriler gibi fiziksel bir geometrinin de empirik olarak doğrulanması ancak dolaylı yoldan olabilir; şöyle ki, teorinin hipotezlerinden, deneysel teste elverişli bir takım mantıksal sonuçlar ya da öndeyiler çıkarılarak gözlem ya da deney sonuçlarıyla karşılaştırılır.Deney sonuçları hipotezden çıkarılan öndeyileri tutarsa, hipotez kanıtlanmış olur. Ancak bu bir ispat değildir.Tersine deney sonuçlarının bir tekinin olumsuz olması hipotezi yalnışlamaya yeter. Tüm hipotezleri böyle kanıtlanan bir teori,olumsuz bir deney sonucu çıkmadığı sürece doğru kabul edilebilir.

Bu dolaylı doğrulama bağlamındadır ki matematik ve mantık empirik bilimler için paha biçilmez değer kazanırlar. Mantık ve matematik olgusal dünya ya ilişkin kendiliklerinden herhangi bir sav ileri sürmezlerse de, Newton mekanğinin yasaları ya da Euclid geometrisinin fiziksel yorumlanmış postulatları gibi somut teorik hipotezlerden, doğrudan deneysel teste vurulabilir. Somut sonuçlar çıkarmayı sağlayan etkin ve vazgeçilmez çıkarın yöntemlerini verirler…

---

Hempel, Carl G. (?) The World of Mathematics (J.R.Newman, Ed.), s.1635-44’ten çeviren: (C.Y.)